2007년 12년 만에 <다이 하드 4.0>으로 부르스 윌리스가 돌아왔다. 1988년 처음 상영된 <다이하드>는 이로써 20년간 지속되는 영화가 됐으며, 브루스 윌리스를 이제 진정한 노장이라고 불러도 될 듯하다. 20년 가까운 세월이 흘렀어도 이 노장의 배짱과 냉소 섞인 유머 그리고 액션에는 변함이 없다. 뉴욕경찰 소속 존 맥클레인(부루스 윌리스)은 늘 잘못된 시간에 잘못된 장소에 가서 테러리스트와 맞닥뜨려 죽도록 고생한다. 게다가 그런 일은 크리스마스 이브처럼 남들이 노는 휴일에 일어난다. <다이하드 4.0>도 미국의 독립기념일인 7월 4일에 벌어지는 이야기이다. 하지만 이야기를 계속하다 보면 점점 과장이 커지고 거짓말이 눈덩이처럼 불어나게 되어 있는 모양이다. 존 맥클레인이 자동차로 헬리콥터를 격추시키고, 낙하산도 없이 비행기에서 뛰어 내리는 것을 보면 그렇다. 더구나 이번 테러의 대상은 전편처럼 특정 건물, 특정 공항, 특정 도시가 아니라 나라 전체다. 미국을 장악하려는 전 정부요원 토마스 가브리엘이 자신의 계획을 저지할 가능성이 있는 모든 해커들을 죽이는 동시에 미국의 네트워크를 공격하기 시작한다. 미국의 교통, 통신, 금융, 전기 등 모든 네트워크가 테러리스트의 손아귀에 들어가고, 미국은 공황상태에 빠진다.
외국의 군대나 외계인이 침입한 것도 아닌데 어떻게 이것이 가능할까? 픽션이기는 하지만, 이런 테러가 가능할 수 있는 것은 모든 시스템이 연결되어 있기 때문이다. 오늘날의 교통, 통신, 금융, 에너지 시스템 등은 대부분 하나의 네트워크로 연결되어 있다. 바로 그것이 문제다.
복잡계라는 말을 심심찮게 듣는다. 이 세상이 복잡하니 복잡계라고 부른다고 해도 무방할 것이다. 그렇다면 역으로 단순계란 무엇일까? 단순계란 ‘명확한 법칙으로 움직임이 정확히 기술되는 시스템’이다. 즉 하나의 원인에 의해 하나의 결과가 결정되는 시스템이다. 기계의 각 부속품이 설계에 따라 움직이는 것과 물질이 분자로 구성되어 있는 것들을 단순계라고 할 수 있다. 따라서 단순계에서는 그 구성요소를 이해하면 그 원리를 모두 이해할 수 있게 된다. 문제는 그런 시스템이 많지 않다는 것이다. 세상의 대부분은 복잡계다. 복잡하게 얽혀 있는 지하철, 전세계를 연결하는 항공망, 인터넷 등이 대표적 복잡계다. 또한 다양한 구성원으로 이루어진 국가와 도시, 경제시스템 그리고 수많은 사람들로 구성된 조직 등 우리가 사는 일상 자체가 복잡계이다.
복잡계를 설명하기 위해 학자들은 많은 새로운 용어를 소개하고 있다. 하지만 우리는 ‘네트워크’라는 비교적 익숙한 한 단어로 이해를 시작해보자. 네트워크라는 단어 자체가 요즘 우리가 만나는 복잡한 세상에 대한 통찰력을 주기도 하지만, 최근 복잡계 과학자들이 밝혀낸 자연과 사회현상을 이해하는 키워드이기도 하다. 네트워크란 상호작용한다는 것을 전제하고 있다. 하나의 새로운 구성요소만 추가되더라도 엄청나게 많은 링크가 새롭게 탄생할 수 있다. 기존에 존재하는 구성원 수만큼의 새로운 연결선이 만들어 질 수 있으니 말이다. 신설공항이 기존의 모든 공항과 항로를 새롭게 개설하는 경우를 생각해 보라. 사실 구성원들간에 상호작용이 없다면 아무리 많은 구성요소가 있다 해도 어떠한 복잡성도 없게 된다. 네트워크에 메트칼프의 법칙이란 것이 있다. 네트워크의 규모가 커짐에 따라 네트워크의 가치는 ‘기하급수적’으로 증가한다는 법칙이다. 예를 들어 단 1명만 인터넷에 연결되어 있다면 인터넷은 아무런 가치가 없다. 그러나 두 명의 인터넷 사용자가 생기면 그 유용성이 2의 제곱이므로 4가 된다. 두 명이 모두 정보를 보내고 받을 수 있음으로 4개의 연결선을 그려볼 수 있기 때문이다. 만약 1백만 개가 연결되었다면 그 유용성은 1백만의 제곱이 된다. 하지만 유용성과 함께 복잡성도 그 숫자만큼 증가하게 되어있다. 복잡계는 수많은 구성요소들로 구성되어있는 집단으로, 이들 구성요소는 독립적으로 존재하는 것이 아니라 끊임없이 상호작용을 주고 받기 때문이다. 이런 결과로 구성요소들을 독립적으로 놓고 봤을 때와는 달리, 새로운 현상과 질서가 나타나게 된다.
카오스이론이 이야기하는 나비효과도 이런 네트워크의 구조라면 이해할 수 있다. 모든 일에는 원인이 있고 결과가 있다. 원인과 결과가 분명하면 정확한 예측이 가능하다. 그러나 사회가 네트워크의 복잡성을 가진다면 어떤 원인이 무슨 결과를 낳는다고 꼬집어 말할 수 없게 된다. 작은 변화가 복잡한 네트워크를 거치면서 확대되어 커다란 변화를 만들어 낼 수도 있기 때문이다. 인터넷의 한 사이트에 올린 동영상이 세상을 놀라게 할 정도의 사회적 이슈를 만들어 내는 현상을 생각해 보면 알 수 있다. 이것이 나비효과다. 나비효과란 초기값의 미세한 차이에 의해 결과가 완전히 달라지는 현상을 의미하며, 미국의 기상학자 에드워드 로렌츠Edward Lorenz가 1972년에 미국 과학부흥협회에서 실시한 강연의 제목인 <예측가능성-브라질에서 한 나비의 날갯짓이 텍사스 돌풍을 일으킬 수도 있는가>에서 유래된 말이다.
세상을 그래서 복잡한 것이라고 말해왔다. 인간사회도 과거부터 복잡계였다. 그런데 왜 오늘날 복잡계라는 것이 화두가 되고 있는 것일까? 세상이 더 복잡해지기라도 했다는 말인가? 그렇다. 복잡해 졌을 뿐 아니라 ‘갑자기’ 복잡해졌다. 그리고 그 원인은 네트워크의 폭발이라고 할 수 있다. <시간의 역사> 저자이자 물리학자인 스티븐 호킹Stephen Hawking은 복잡성이 생기는 이유를 다음과 같이 설명하고 있다.
“증가한 변수들이 서로 예측할 수 없는 방법으로 상호작용하기 시작한다(An increasing number of independent variables begin interacting in interdependent and unpredictable ways).”
어둠이 깔린 지구본을 바라보고 있다고 하자. 그리고 고속도로나 항로로 두 개 이상 연결된 도시에만 불이 들어온다고 상상해 보자. 역사의 초기에는 여기 저기 떨어진 곳에서만 불이 반짝이고 있었을 것이다. 계속해서 고속도로를 만들고 새로운 항로를 만들다 보면 갑자기 지구본 전체에 불이 동시에 들어오는 듯한 상황을 목격할 수 있게 된다. 여기저기 떨어져 있던 연결고리가 붙으면서 갑자기 지구 전체가 모두 연결되는 분기점이 있기 때문이다. 도시가 서로 연결되다 보면 홀로 떨어져 있던 하나의 도시가 이미 다른 도시들과 잘 연결된 도시를 만나는 일이 생긴다. 이런 경우에는 하나의 항로만 개설하였는데 지구에 존재하는 모든 도시와 만나지는 결과를 만든다. 그렇다 보면 점진적으로 연결되는 네트워크가 갑자기 전체가 연결되는 듯한 현상으로 나타날 것이다.
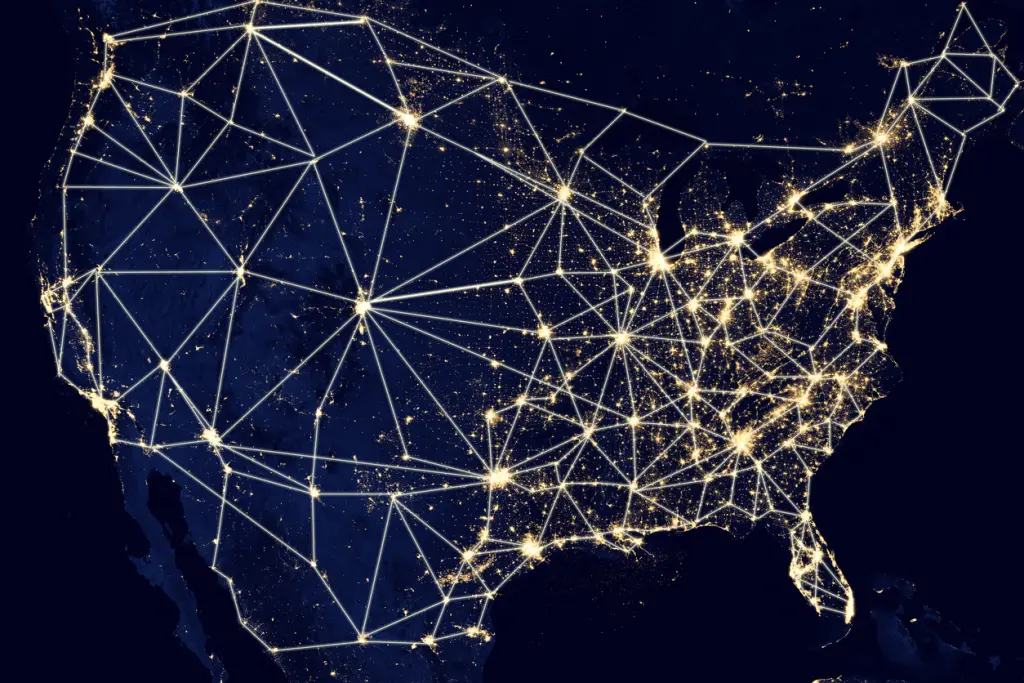
이런 현상을 <부의 기원>의 저자 에릭 바인하커는 ‘네트워크의 폭발’이라고 표현한다. 변화는 점진적으로 일어나는 것이라 인식하기 쉽다. 하지만 변화라는 것 차제가 처음에는 미미하게 그리고 서서히 진행되는 것처럼 보이지만, 어느 순간 ‘탁’하고 터지는 임계점이 있기 마련이다. 임계란 어떤 경계에 다 달았다는 말로서, 말콤 글래드웰Malcom Gladwell이 이야기하는 ‘티핑 포인트’ 라는 의미로 해석할 수 있다. 다시 말해 액체에서 기체로 변하듯 급속하게 변화하는 전환점 또는 분기점이 바로 임계점(Critical Point)이며 그 전환점 바로 직전의 상태가 임계상태다. 탁자 위에 모래알을 한 개씩 뿌려보면 모래더미가 형성된다. 이 모래더미는 점점 쌓이다가 경사가 가팔라지면 모래알은 경사면을 타고 조금씩 흘러내리게 된다. 그러다 어느 순간 작은 모래알 하나에도 모래산은 와르르 무너져 더 낮은 상태가 되기도 한다. 이처럼 별 것 아닌 원인에도 격변이 일어날 수 있는 상태가 ‘임계상태’다. 구성원간에 긴밀히 연결되어 있기 때문에 생기는 결과로 우리가 흔히 이야기하는 ‘연쇄반응’이나 ‘도미노 현상’과 다르지 않다. 다만 더 이상 견딜 수 없는 임계상태에서는 아주 작은 것에도 영향을 받을 수 있다는 특성에서 도미노 현상과는 차이가 있다. 아니 도미노라는 것이 인위적으로 만들어 놓은 임계상태이기 때문에 아주 작은 힘으로도 전체가 함께 무너지는 것이라고 이해해도 좋을 것 같다. 이처럼 임계상태에서 더 이상 견디지 못하고 ‘폭발’해 버리는 현상은 자연과 인간의 삶 곳곳에 깔려 있다. 쉽게 눈사태를 상상해 보면 된다. 아니 참다 못해 폭발해 버린 나의 분노를 생각해 보아도 짐작이 가능하다. 참고 있다고 해서 나의 분노가 사라진 것은 아니다. 내 속에서 커져 가던 화나는 감정이 그 한계를 넘어서면 밖으로 표출되고 만다. 그 임계점이 너 높은 사람일수록 더 나은 삶을 살 수 있기는 하다. 지난 일을 돌이키며 “더 참을걸” 하며 후회하는 것을 보면 그렇다. 마크 뷰케넌Mark Buchanan은 그의 저서 <세상은 생각보다 단순하다>에서 임계상태를 나타내는 현상들은 지구상의 갖가지 현상들에도 그대로 적용됨을 지적한다. 지진, 전쟁, 산불, 태풍, 대량 멸종, 교통 체증, 주가 폭락, 심지어 논문인용에까지 일어나는 현상이라는 것이다.
오늘날 우리가 경험하고 있는 세계화 그리고 인터넷의 세상도 그렇게 만들어 졌다. 그렇다면 오늘날 우리들의 네트워크는 어떤 모양을 하고 있을까? 많은 과학자들의 연구결과, 자연계의 네트워크나 사회적 네트워크 모두 유사한 모습을 하고 있다는 것을 알아냈다. 그리고 그 모습은 전에 얼핏 살펴본 오늘날의 항공망과 비슷하다. 모든 도시가 최소한 하나의 연결을 가진 네트워크의 모습을 하고 있지만, 모두 비슷한 숫자의 링크를 가지고 있지는 않다. 완전히 임의적이지도 않지만 분명한 규칙성도 없이 몇 개의 공항에 노선이 편중적으로 집중되어 있는 모습을 하고 있다. 예들 들어 미국의 항공망은 시카고 오헤어공항과 뉴욕 JFK공항처럼 연결선이 많은 몇 개의 허브공항과 많은 작은 수의 링크를 가진 공항들로 이루어져 있다. 인터넷도 몇 개의 거대한 포탈사이트가 허브 역할을 하면서, 작은 링크를 가지고 있는 수많은 사이트들로 구성되어 있다. 인간이 만들어 내는 사회적 네트워크나 단백질이나 세포 등 자연계에서 보여지는 네트워크도 모두 이런 형태를 보여주고 있다. 뇌세포의 연결된 그림을 엿보기 위해 전세계의 항공망을 상상한 것과는 반대로, 세상이 연결된 모습을 실감하기 위해서 이제는 뇌세포로 연결된 네트워크를 머리 속에 그려봐야 할지도 모르겠다.
정하웅 한국과학기술원(KAIST) 물리학과 교수는 “전체 인터넷 네트워크 절반이 1%의 중요한 허브와 관련돼 있다”면서, ‘월드와이드웹의 기본 아이디어가 연결이 집중되는 중앙 허브를 따로 두지 않는다는 것이었음에도 불구하고 이러한 허브들이 자연스럽게 발생한 것’이라는 점을 강조한다. 따라서 <다이하드 4.0>에서 테러리스트는 모든 사이트를 공격할 필요가 없어진다. 중요한 허브만 잘 알고 공격할 경우 전체 네트워크를 마비 상태로 만들 수 있기 때문이다. 인터넷의 구조를 잘 알고 있는 누군가가 중요한 노드 1%만 공격해도 전체 인터넷 기능의 절반이 마비되고 4% 정도를 공격하면 인터넷은 연결이 완전히 끊긴 조각으로 파편화될 수 있다.
과학자들은 이런 네트워크를 척도 없는 네트워크(scale-free network)라고 부른다. 척도가 없다는 말은 전형적인 크기가 없다는 뜻이며 그런 곳에서는 평균이란 말이 의미가 없게 된다. 또 다른 중요한 의미가 숨겨져 있지만, 우선 평균이 의미가 없다는 말에 집중해보자. 우리는 자연계에서 발견되는 대부분의 현상이 정규분포를 이루고 있다는 점을 지적하였다. 단순하게 이야기하면 관찰대상이 평균에 대부분이 모여있는 현상이다. 그런데 네트워크로 모든 것이 연결되어 상호작용하는 복잡계에서는 큰 것은 극단적으로 드물고 조그만 것이 매우 많이 나타나는 현상이 발견된다. 인터넷의 허브 사이트와 항공망의 대형 공항이 허브를 이루고 있는 형태가 그렇다. 이런 현상을 과학자들은 멱함수 또는 거듭제곱법칙이라고 부른다.
거듭제곱 법칙이라는 말에 혼란스러워 할 필요는 없다. 단순히 하나 둘 증가하거나 감소하는 것이 아니라, 배수로 변하는 상황을 생각해 보면 된다. 한쪽은 높고 한쪽이 낮은 곡선을 상상해보자. 차이가 많이 나는 크기를 비교할 때 사용했던 로그함수를 이용하면, 거듭제곱 분포의 곡선을 직선으로 표시할 수 있다. 이 그림을 다시 말로 표현하면, 거듭제곱 법칙이란 어떤 현상의 규모와 발생 빈도가 반비례한다는 것을 의미한다. 예를 들어 강도가 약한 지진은 자주 일어나지만 도가 센 지진의 발생 빈도는 아주 적다. 실제로 거듭제곱 분포를 처음 발견한 곳이 지진에 대한 연구였으며, 과학자들은 아주 구체적으로 규모가 2배로 큰 지진은 작은 지진이 발생할 확률에 비해 정확하게 4배씩 줄어든다는 것을 발견한다. 흥미로운 것은 많은 사회와 자연현상에서 이런 분포를 찾아낼 수 있다는 것이다. 마크 뷰캐넌은 냉동감자의 파편에서 이 법칙을 발견한다. 감자를 벽에다 세게 내동댕이쳐 파편조각을 낼 수 있을 것이다. 그런 다음 아주 작은 조각부터 큰 조각들을 무게 별로 모아 숫자를 세어보면, 큰 조각 수는 아주 적고 작은 조각은 아주 많이 만들어진다. 다시 말해 작은 조각으로 갈수록 그 숫자가 많아진다는 말이다. 그런데 그냥 많아지는 것이 아니고 작은 조각의 수는 자신의 무게 두 배 되는 감자 조각수보다 딱 6배 많아진다. 그래서 거듭제곱법칙이라고 부르는 것이다.
거듭제곱법칙에 의해 이제 우리는 파레토 법칙을 자연적인 현상으로 받아들이고 그 의미를 더 잘 이해할 수 있게 되었다. 파레토 법칙이란 ‘전체 결과의 80%가 전체 원인의 20%에서 일어나는 현상’을 가리킨다. 기업 전체의 20%에 해당하는 사람들이 80%의 일을 하고, 판매중인 상품들 중 상위 20% 인기제품에서 80%의 수익을 올린다는 것 등이 그것이다. 또한 상위 20%의 고객이 전체 매출의 80%를 만들어준다는 것도 파레토 법칙이다. 파레토 법칙을 처음 제시한 경제학자 파레토Vilfredo Pareto가 ‘이탈리아 인구의 20%가 이탈리아 전체 부의 80%를 가지고 있다’고 이야기한 것처럼 부의 불평등 현상을 이야기할 때 사용하기도 한다. 이런 현상을 그래프로 그려보면, 바로 거듭제곱법칙의 모습을 하고 있다. 가난한 사람은 많고, 중산층은 넓은 구간에 걸쳐 분포되어 있는 반면 매우 부자인 사람들은 적다. 하지만 적은 부자들이 부의 대부분을 차지하고 있는 것이다. 거듭제곱 법칙은 결국 불평등의 법칙이기도 하지만, 아쉽게도 그런 현상은 인터넷에서, 우리의 몸 안에서 그리고 사회현상에서 일어나고 있다.
자연현상과 사회현상에서 이처럼 많은 거듭제곱의 분포와 정규분포가 함께 존재한다면, 그들간에 무슨 관계가 있지 않을까? 확실하지 않다. 아마도 거듭제곱과 정규분포는 아마도 관찰의 범위와 시각의 차이에서 나타나는 것으로 추측해 볼 수는 있다. 예들 들어 거듭제곱법칙은 어쩌면 전체가 아닌 부분에서 나타나는 현상일 수도 있다. 다시 말해 분포의 전체가 아닌 꼬리부분만 집중적으로 관찰할 때 거듭제곱의 형태를 볼 수 있을지도 모른다는 말이다. 지진의 경우 지각이 움직이는 쪽만 관찰하는 것이다. 평형을 이루고 있는 것이 대부분이라는 생각을 한다면, 지진은 평형이라는 평균을 중심으로 땅이 움직이는 쪽의 꼬리부분이 된다. 실제로 주식 가격 변동의 분포가 그렇다. 보스톤의 진 스탠리Gene Stanley는 1994년부터 1995년까지 5분마다 미국의 주가가 변하는 것을 관찰하여, 가격변동 분포의 꼬리부분이 거듭제곱 법칙을 따르고 있다는 것을 알아냈다. 자연에서 관찰되는 크기나 속도 무게 등 독립적으로 존재하는 것은 정규분포를 이루고 있지만, 서로 상호작용하여 만들어 내며 변하는 시스템은 거듭제곱의 법칙을 따르고 있다.
이런 관점에서 보면 거듭제곱 법칙은 변화에 관한 것인지도 모른다. 변화라는 곳에는 점진적으로 움직이다가 폭발하듯 변하는 임계점이 존재한다. 어느 정도 규칙적인 움직임을 보이다가도, 한 순간에 규칙성이 깨진 이후에는 복잡하고 불규칙한 모습을 보일 수 있다는 말이다. 하지만 카오스인 것처럼 보이는 세상에도 규칙성이 존재한다.
척도 없는 네트워크라는 말에서 “척도가 없다”는 말의 또 다른 의미는 네트워크의 한 부분 어디에 가 있다고 하더라도 같은 모습으로 보인다는 것이다. 이 말을 다르게 표현하면 척도와 상관없이 어느 곳에서도 유사한 현상을 관찰할 수 있다는 말이 된다. 세상이 아무리 복잡해도 프랙탈의 구조를 이루고 있다는 말과도 같은 말이다. 마크 뷰캐넌의 냉동감자 이야기를 다시 떠올려 보자. 큰 조각 중 하나를 골라 그것보다 한 단계 무거운 감자조각의 수를 세어보면, 1/6 수준으로 숫자가 줄어든다. 다시 한 단계 가벼운 조각의 수를 헤아려보면 그 숫자는 6배가 많아진다. 이제 아주 작은 조각하나를 골라보자. 그리고 마찬가지로 그 보다 무거운 것과 가벼운 것의 숫자를 세어보면 각각 1/6 그리고 6배의 수가 나타난다는 것이다. 마크 뷰캐넌의 표현처럼 우리가 몸의 크기를 여러 단계의 감자조각의 크기로 줄여가면서 관찰한다면, 어느 크기에서나 거의 같은 풍경을 볼 수 있다는 말이다. 그러니까 척도가 의미가 없는 것이며, 그런 네트워크는 척도 없는 것이 된다.
복잡계 과학도 이처럼 규칙성에 집중한다. 그리고 그 응용범위도 자연과학이나 공학 분야에 그치지 않고, 경제학, 사회학 등의 인문 사회과학, 예술 분야에까지 이른다. 그런 성과는 역으로 물리학, 생물학, 경제학 그리고 여러 다른 분야들로부터 수학적, 통계학적 기법들을 통합하여 얻어진 것이다. 복잡계 과학이나 복잡계 경제학의 학자들은 세상을 보는 다양한 시각을 인정하고 또 그를 활용하여 이 복잡한 세상에 대한 더 나은 이해를 얻어낸다. 우리가 비교적 까다로울 수 있는 복잡계와 네트워크가 가지는 의미를 이해하고자 하는 이유도 어쩌면 그런 과정에서 세상을 보는 새로운 통찰력을 가질게 될지도 모르기 때문이다. 이미 언급한 뇌세포와 기억이라는 정보도 이런 모습을 하고 있고, 앞으로 논의할 사람들이 만들어 내는 인간관계도 이런 네트워크의 형태를 가지고 있다.
Knowledge comes by taking things apart: analysis. But wisdom comes by putting things together~ John Morrison 지식은 분석을 통해 얻어지지만, 지혜는 그 모든 것의 통합을 통해 얻어진다.~ 존 모리슨


답글 남기기